10 min to read
02. 쉐이더 함수정리
쉐이더 함수정리

shader math function(수학함수)
수학함수
lerp(a,b, t) : 선형보간 함수 t는 0~1사의 값 0의 가까우면 a값에 가까워지고 1의 가까우면 b의 값의 가까워진다
lerp(1, 5, 0) // 1
lerp(1, 5, 0.5)// 3
lerp(1, 5, 1)// 5
radians(x) : x의 라디안 값 반환 (60분법)
radians(180) // PI
radians(360) // 2PI
radians(1) // PI/180
saturate(x) : 0 ~ 1 넘는 값을 잘라버리는 함수
saturate(10) // 1
saturate(0.5) // 0.5
saturate(0) // 0
saturate(-1) // 0
abs(x) : 절대값을 반환하는 함수
abs(-10) // 10
abs(10) // 10
clamp(a, b, c) : a = 현재값, b = 최소값, c = 최대값, a를 b와 c의 값으로 범위를 제한 시킨다
clamp(10, 0, 5) //5
clamp(-1, 0, 5) //0
clamp(3, 0, 5) // 3
max(a,b) : a와 b중에 큰 값 반환
max(10, 5)// 5
max(20, 10)// 10
min(a, b) : a와 b중에 작은 값 반환
min(-1, -3) // -3
min(-5, -10) // -10
min(5, 10) // 10
sign(x) : x에 대해 부호를 반환합니다 양수의 경우 1, 0의 경우 0, 음수의 경우 -1을 반환 합니다.
sign(-3) // -1
sign(0) // 0
sign(10) // 1
step(x,y) : x <= y 일때 1을 반환 아니면 0을 반환한다
step(10, 10) // 1
step(10, 9) // 0
step(9, 10) // 1
acos(x) : 아크 코사인 함수 각도를 구할때 많이씀, cos를 적용했을 때 x가 나오는 라디안 각도 값을 반환 합니다.
acos(x)
asin(x) : 아크 사인 함수 각도를 구할때 많이씀, sin을 적용했을 때 x가 나오는 라디안 각도 값을 반환 합니다.
asin(x)
atan(x) : 아크 탄젠트 함수 각도를 구할때 많이씀, tan을 적용했을 때 x가 나오는 라디안 각도 값을 반환합니다.
atan(x)
atan2 : tan을 적용했을 때(x,y)가 나오는 라디란 각도 값을 반환합니다.
atan2(y, x)
ceil : 무조건 올림함수
ceil(10.1) // 11
ceil(10.6) // 11
ceil(10) // 10
cos : 코사인 값 반환
cos(x)
cosh : 라디안 x의 하이퍼볼릭 cos값을 반환합니다.
cosh(x)
exp : x를 인수로 하는 e^x 값을 반환합니다. e(오일러 상수, 자연상수)
console.log(Math.exp(0));
// expected output: 1
console.log(Math.exp(1));
// expected output: 2.718281828459 (approximately)
console.log(Math.exp(-1));
// expected output: 0.36787944117144233
console.log(Math.exp(2));
// expected output: 7.38905609893065
degress(x) : 라디안 값을 각도로 반환
degress(PI) // 180
degress(2*PI) // 360
degress(PI/180) // 1
exp2(x) : 밑수가 2인 지수 2^x
exp2(1.0) // 2.000000
exp2(1.2) // 2.297397
exp2(1.4) // 2.639016
exp2(1.6) // 3.031433
exp2(1.8) // 3.482202
exp2(2.0) // 4.000000
exp2(2.2) // 4.594793
exp2(2.4) // 5.278032
exp2(2.6) // 6.062866
exp2(2.8) // 6.964405
exp2(3.0) // 8.000000
floor : 무조건 내림함수
floor(10.5) // 10
floor(10.9) // 10
floor(10.8) // 10
floor(10) // 10
fmod(x) : 나눠서 실수부분 반환하는 함수
fmod() //?
frac(x) : x의 소숫점 반환하는 함수
frac(x)
frexp : x의 값에 대한 지수 반환?
frexp(x)
isfinite(x) : 무한대, 주어진 값이 유한수인지 판별, 인자가 양 또는 음의 Infinity거나 NaN이면 false, 아니면 true.
isfinite(Infinity); // false
isfinite(NaN); // false
isfinite(-Infinity); // false
isfinite(0); // true
isfinite(2e64); // true
isfinite(910); // true
isfinite(null); // true, would've been false with the
// more robust Number.isfinite(null)
isfinite('0'); // true, would've been false with the
// more robust Number.isfinite("0")
sinf(x) : 함수의 x 가 무한대 이면, 0이 아닌 값을 반환 한다.
isinf(0) // 0
isinf(910) //0
isinf(Infinity) //
isinf(-Infinity) //
isnan(x) : 함수의 x 가 NaN 이면 true, 다른 값이면 flase를 반환 한다.
isnan(NAN) //true
isnan(0) // false
isnan(-10) // flase
ldexp(x, exp) : x * 2^exp, 성공 할 경우, 위의 수식 결과 값을 반환 한다.
만약 인자값x가 NaN 이면, NaN이 반환 된다.
만약 인자값x가 ±0 또는 ±Inf 이면 ,x가 반환 된다.
만약 인자값x가 0 이면, x가 반환 된다.
log(x) : x의 자연로그 값을 구한다.
성공할 경우, x의 자연 로그값을 반환 한다.
만약 인자값x가 NaN 이면, NaN이 반환 된다.
만약 인자값x가 1 이면, +0 이 반환 된다.
만약 인자값x가 양의 무한대 이면, 양의 무한대가 반환 된다.
만약 인자값x가 0이면, 부호 오류가 발생하고, -HUGE_VAL, -HUGE_VALF 또는 -HUGE_VALL 이 반환 된다.
만약 인자값x가 음수 (음의 무한대 포함) 이면, 도메인 오류가 발생하고, NaN이 반환 된다.
log2(x) : x값에 대한 밑수가 2인 로그 값을 반환
성공할 경우, 밑수가 2인 로그를 반환한다.
만약 인자값x가 NaN 이면, NaN이 반환 된다.
만약 인자값x가 +Inf 이면, x이 반환 된다.
만약 인자값x가 1이면, +0 이 반환 된다.
만약 인자값x가 ±0 이면, 부호 오류가 발생하고, -HUGE_VAL, -HUGE_VALF, 그리고 -HUGE_VALL 이 반환 된다.
log10(x) : x의 밑수 10인 로그 값을 반환
성공할 경우, x의 밑수 10인 로그값을 반환 한다.
만약 인자값x가 NaN 이면, NaN이 반환 된다.
만약 인자값x가 1 이면, +0 이 반환 된다.
만약 인자값x가 +Inf 이면, x이 반환 된다.
만약 인자값x가 0이면, 부호 오류가 발생하고, -HUGE_VAL, -HUGE_VALF 또는 -HUGE_VALL 이 반환 된다.
만약 인자값x가 음수 (음의 무한대 포함) 이면, 도메인 오류가 발생하고, NaN이 반환 된다.
modf : 실수 값에서 정수부와 소수부를 구하는 함수
pow(x) : x의 값에 대한 x^x 값을 반환
pow(2) // 4
pow(3) // 9
pow(5) // 25
pow(10) // 100
round(x) : 반올림 함수
round(5.1) // 5
round(5.5) // 6
round(5.5111) // 6
round(5.6) // 6
sin(x) : 사인 각도에 따른 라디안 값 반환
sincos(x) : tan??
sinh(x) : 쌍곡선 사인 함수
smoothstep
sprt(x) : x값의 대한 제곱근 반환
sqrt(4) // 2
sqrt(9) // 3
sqrt(2) // 1.414 root2
tan(x) : 탄젠트 라디안 값 반환
tanh(x) : 이 함수는 x의 값이 라디안 범위 일때 쌍곡선 탄젠트 값을 계산한다. (x , -1 <= x <= 1)
성공할 경우 tanh함수는 x의 쌍곡선 탄젠트 값을 반환 한다.
만약 인자값x가 NaN 이면, NaN이 반환 된다.
만약 인자값x가 ±0 이면, x를 반환 된다.
만약 인자값x가 subnormal이면, 범위 오류가 발생하고, x 이 반환된다.
만약 인자값x가 ±Inf 이면, ±1 이 반환된다.
벡터함수(Vector Function)
dot(a, b) : 내적 함수 a, b벡터에 대한
flaot3 v1, v2;
dot(v1, v2) // v1(1,0,0), v2(1,0,0) output = 1
dot(v1, v2) // v1(1,0,0), v2(0,1,0) output = 0
dot(v1, v2) // v1(1,0,0), v2(1,1,0) output = 0.5
dot(v1, v2) // v1(1,0,0), v2(-1,0,0) output = -1
reflect : 반사벡터를 구하는 함수
all
any
cross : 외적함수
faceforward : 표면에서 노말벡터
distance : 거리함수
length : 길이?
lit
normalize : 정규화 함수
refract
행렬함수
mul : 행렬곱셈함수
transpose
determinant : 행렬
텍스쳐함수
tex1D, tex2D(텍스처와 uv값을 넘기면 해당하는 rgba색상을 반환하는 함수),
tex3D, texCUBE
tex11 Dproj, tex2Dproj, tex3Dproj, texCUBEproj,
tex1Dbias, tex2Dbias , tex3Dbias, texCUBEbias
기타함수
noise
0.Lambert Lighting(확산 조명)
확산광 = 빛의세기 x 물체의색 X (Normal . LightingDir)
받아올 Sementic(시멘틱)
POSITION, NORMAL
0.1 BlinFong Half Vector(블린퐁 하프벡터)
| hlaf = E + L / | E + L |
반사광 = 빛의세기 x 물체의색 + 빛의세기 x 물체의색 * (Normal . Lighting) + 빛의세기 x 물체의색 + (Normal . half) 제곱
0.2 쿡, 토런스 반사 모델(금속 표면면)
퐁에 의한 반영 반사 모델은 빛의 반사를 간단한 계산으로 표현할 수있는 훌륭한 것이지만.
어차피 퐁의 경험과 직감에 의지한 이론이므로 싸구려 플라스틱 같은 질감이라 현실감이 없습니다
그래서 토런스(Torrance), 스패로우(Sparrow), 블린(Blinn), 쿡(Cock) 등의 선각자들의 표면의 거친 정도를 표현 할수 있는 좀더 좋은 반사 모델을 생각했습니다
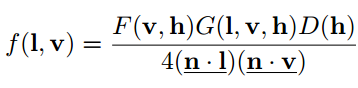

Comments